P Method Of Convergence

Guo B Heuer N. If g and g are continuous on the interval a b containing the root alpha and if mathrmmax_a x b mid gx mid 1 then the fixed point iterates x_n1 gx_n will converge to alpha.

Leadership In A Vuca World Leadership Strategies Leadership Business Leadership

Therefore p p a.

P method of convergence. In this paper we obtain for p 3 explicit p-dependent convergence regions that significantly expand existing explicit convergence regions. H method 2. Therefore the higher the global order of accuracy the faster the convergence rate of thenumerical method.

P 1 2 p a p p a. I fp kg1 k1 monotonically decreasing. Using the default convergence criteria gives a noticeable discontinuity in stress contours across element boundaries indicating poor accuracy in the computed stresses and the total strain energy looks as though it would continue change if the p-levels were incremented.

The sequence ak with ak 2-k which was also introduced above converges with order p for every number p. I Newtons Method quadratically convergent lim k1 jp k p aj p k 1 p a 2. Lets consider the meaning of this statement in more depth.

Motivated by the above results we define D-iteration by and where and. We conclude that for hsu ciently small the trapezoidal method is stable and therefore convergent with Oh2 global error. In the finite element FE analysis h and p-type element type are used for convergence purpose.

Define the matrices P and Q by P 7 77 L - UTU Q 7 UTI U - LTL. It follows that it is generally necessary to solve a nonlinear equation to obtain y n1 from y n. Rate of Convergence De nition 1.

For p 3 however the convergence region will be much smaller. It is said to converge exponentially using the convention for discretization methods. Equation 42 becomes 43 w2P - ww - 1Q 0.

If a sequence x 1x 2x nconverges to a value rand if there exist real numbers 0 and 1 such that 1 lim n1 jx n1 rj jx n rj then we say that is the rate of convergence of the sequence. However there are some difficulties with the method. In 2015 Sainuan 10 constructed a new iteration called P-iteration and showed that this iteration converges faster than S-iteration for the class of continuous nondecreasing functions.

P k p a 1 2 p k 1 a p k 1 p a p p k 1 2 2p k 1 0. The optimal rate of convergence of the p-version of the boundary element method in two dimensions. I lim k1p k def p exists and satis es Newton Iteration.

P k1 p k 1 2 p k a p k p k a p2 k 2p k 0. For a first-order accurate method p1 we expect. If A is X163-5y-7z.

To evaluate the convergence select p-Convergence. However it only converges linearly that is with order 1 using the convention for iterative methods. For p 2 the convergence region is the whole region for which A 1 2 is defined.

The trapezoidal method constrasts with Eulers method because it is an implicit method due to the evaluation of fty at y n1. Corollary 1 Convergence Criterion of the Fixed Point Method. P method The h- and p- versions of the finite element method are different ways of adding degrees of freedom dof to the model Figure 1.

A similar condition may be derived from equation 41 in the same way. The rate of convergence of False position p 1 linear convergence Netwon s method p 2 quadratic convergence Secant method p 1618. P Q A AT.

RATE OF CONVERGENCE OF BISECTION METHOD. P-iteration is defined by and where and. Newtons Method for p a converges quadratically if p 0 0 I fp kg1 k1 bounded below by p a.

This additional computational e ort is o set by the fact that. If a method has global order of accuracyp in the limitDt0 if we shrink the time step by a factor of two we can expect the worst case error in the approximation todecrease by a factor of 2p. Henee SOR will converge for w 1 if P 0.

Development of a formula to estimate the rate of convergence for these methods when the actual root is not known. Choice of using either of the method depends on type of. As the method converges on the root the difference between the root and the approximation is squared the number of accurate digits roughly doubles at each step.

Currently two types method are used to demonstrate the numerical convergence of the solution. Newtons method is a powerful techniquein general the convergence is quadratic. Z 129-3x6y symmetric positive dominant then s j - D-1 L U now by using the Jacobi iteration formulai with is convergent and the Jacobi iteration will converge initial approximation 0 0 0 we get otherwise the method will converge frequently.

Theorem 2 indicates that conditions 41 and 42 will be. Fixed point iteration p 1 linear convergence The rate value of rate of convergence is just a theoretical index of convergence in general. Such a region is called a convergence region for Newtons method.

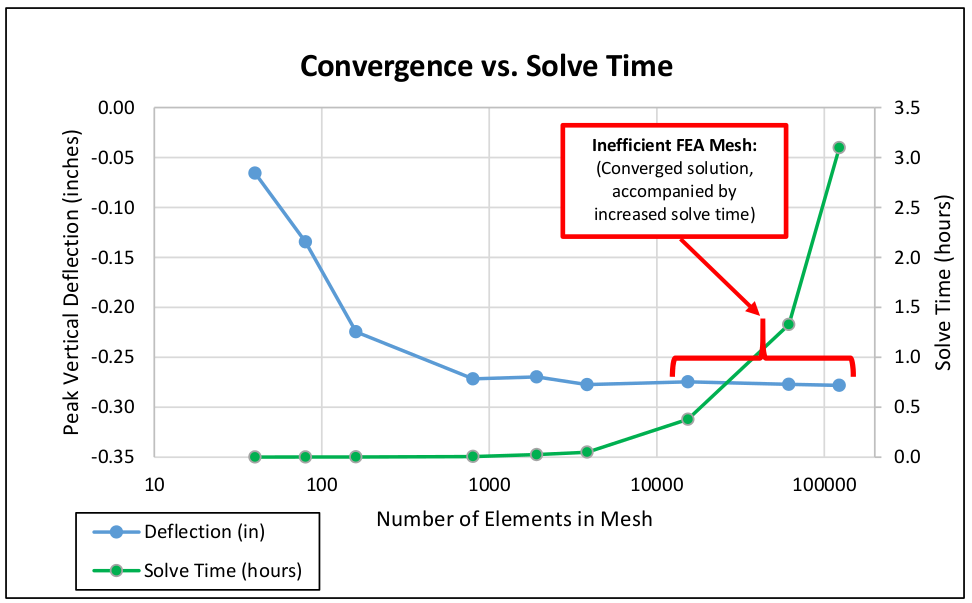
Finite Element Analysis Convergence And Mesh Independence

Moving Average Convergence Divergence Macd Definition Technical Analysis Indicators Moving Average Technical Analysis

Moving Average Convergence Trading Method Macd Made Simple Bonniegortler Com Moving Average Online Trading Convergence

Image 34 Jpg Ricky Tims Convergence Quilts Geometric Quilt Bargello Quilts Sunflower Quilts

Moving Average Convergence Trading Method Macd Made Simple For The Simple Mind Bonniegortler Com Online Trading Moving Average Convergence

Studyblr Booklr Appblr Calculus Notes Inspiration School Notes

Solution Convergence An Overview Sciencedirect Topics

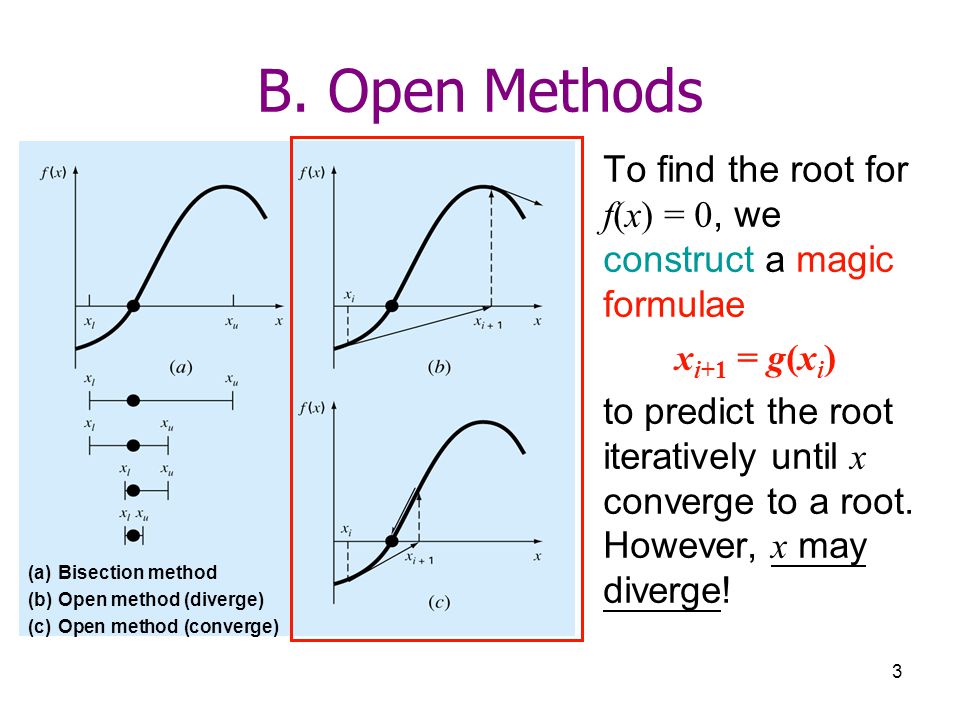
Open Methods Part 1 Fixed Point Iteration Newton Raphson Methods Ppt Video Online Download

Divergence Convergence In Design Thinking Thinking In Ways You May Not Be Used To Think503x Cour Design Thinking Process Design Thinking Systems Thinking

And Yet Another View Of The Funnel This Variation On Pugh S Illustration Emphasizes The Fact That The Process Is The Same As One Converges To Ever Finer Level

Pin On To Do List