Method L-bfgs

The L-BFGS method Liu Nocedal 1989 has tradition-ally been regarded as a batch method in the machine learn-ing community. Methods Limited-memory BFGS L-BFGS4 is one of the frequently used optimization methods in practice5.

The L Bfgs Two Loop Recursion Algorithm For Calculating The Action Of Download Scientific Diagram

And people are still developing modified L-BFGS for mini-batch approach.

Method l-bfgs. Function nl_eval_init starts processes with NetLogo instance Function nl_get_param_range returns parameters lower and upper values as they are defined in experiment object. The initial value must satisfy the constraints. The L-BFGS algorithm is a very efficient algorithm for solving large scale problems.

The L-BFGS-B algorithm is an extension of the L-BFGS algorithm to handle simple bounds on the model Zhu et al. The L-BFGS algorithm named for limited BFGS simply truncates the BFGSMultiply update to use the last m input differences and gradient differences. Thesealgorithmic ingredients can be implemented it seems onlyby using very large batch sizes resulting in a costly.

Also I doubt L-BFGS efficiency when using mini-batches. L-BFGS method 4353 that strives to reach the right balance between e cient learning and productive parallelism. This is promising and provides evidence that quasi-Newton methods with block updates are a practical tool for unconstrained minimization.

This uses a limited-memory modification of the BFGS quasi-Newton method. I used this book by JNocedal and SWright as a reference. 1995 which allows box constraints that is each variable can be given a lower andor upper bound.

If disp is None the default then the supplied version of iprint is used. L-BFGS is a pretty simple algorithm. Method L-BFGS-B is that of Byrd et.

From the mathematical aspect the regular L-BFGS method does not work well with mini-batch training. This is because quasi-Newton algorithmsneed gradients of high quality in order to construct usefulquadratic models and perform reliable line searches. This method also returns an approximation of the Hessian inverse stored as hess_inv in the OptimizeResult object.

If non-trivial bounds are supplied this method will be selected with a warning. This range will be used as optimization constraints in L-BFGS-B method. If non-trivial bounds are supplied this method will be selected with a warning.

The initial value must satisfy the constraints. Like most iterative optimisation algorithms it amounts to. Newtons Method solves for the roots of a nonlinear equation by providing a linear approximation to the nonlinear equation at.

L-BFGS-B borrows ideas from the trust region methods while keeping the L-BFGS update of the Hessian and line search algorithms. The original L-BFGS algorithm and its. If disp is not None then it overrides the supplied version of iprint with the behaviour you outlined.

Minimize a scalar function of one or more variables using the L-BFGS-B algorithm. Method L-BFGS-B is that of Byrd et. 1995 which allows box constraints that is each variable can be given a lower andor upper bound.

This uses a limited-memory modification of the BFGS quasi-Newton method. A readable implementation of L-BFGS method in modern C. Nowadays one can find an explanation of it in pretty much any textbook on numerical optimisation eg.

The Broyden-Fletcher-Goldfarb-Shanno BFGS method is the most commonly used update strategy for implementing a Quasi-Newtown optimization technique. Method BFGS uses the quasi-Newton method of Broyden Fletcher Goldfarb and Shanno BFGS pp. BFGS has proven good performance even for non-smooth optimizations.

Newtons method was first derived as a numerical technique for solving for the roots of a nonlinear equation. If you google the papers of L-BFGS for mini-batch training this is probably still an ongoing research topic. It uses the first derivatives only.

In this paper we study the L-BFGS implementation for billion-variable scale prob-lems in a map-reduce environment. This means we only need to store sn sn 1 sn m 1 and yn yn 1 yn m 1 to compute the update. At present due to its fast learning properties and low per-iteration cost the preferred method for very large scale applications is the stochastic gradient SG method 1360.

Experimental results from 6 show that their limited memory method Stochastic Block L-BFGS often outperforms other state-of-the-art methods when applied to a class of machine learning prob-lems.

1 L Bfgs And Delayed Dynamical Systems Approach For Unconstrained Optimization Xiaohui Xie Supervisor Dr Hon Wah Tam Ppt Download

The L Bfgs Two Loop Recursion Algorithm For Calculating The Action Of Download Scientific Diagram

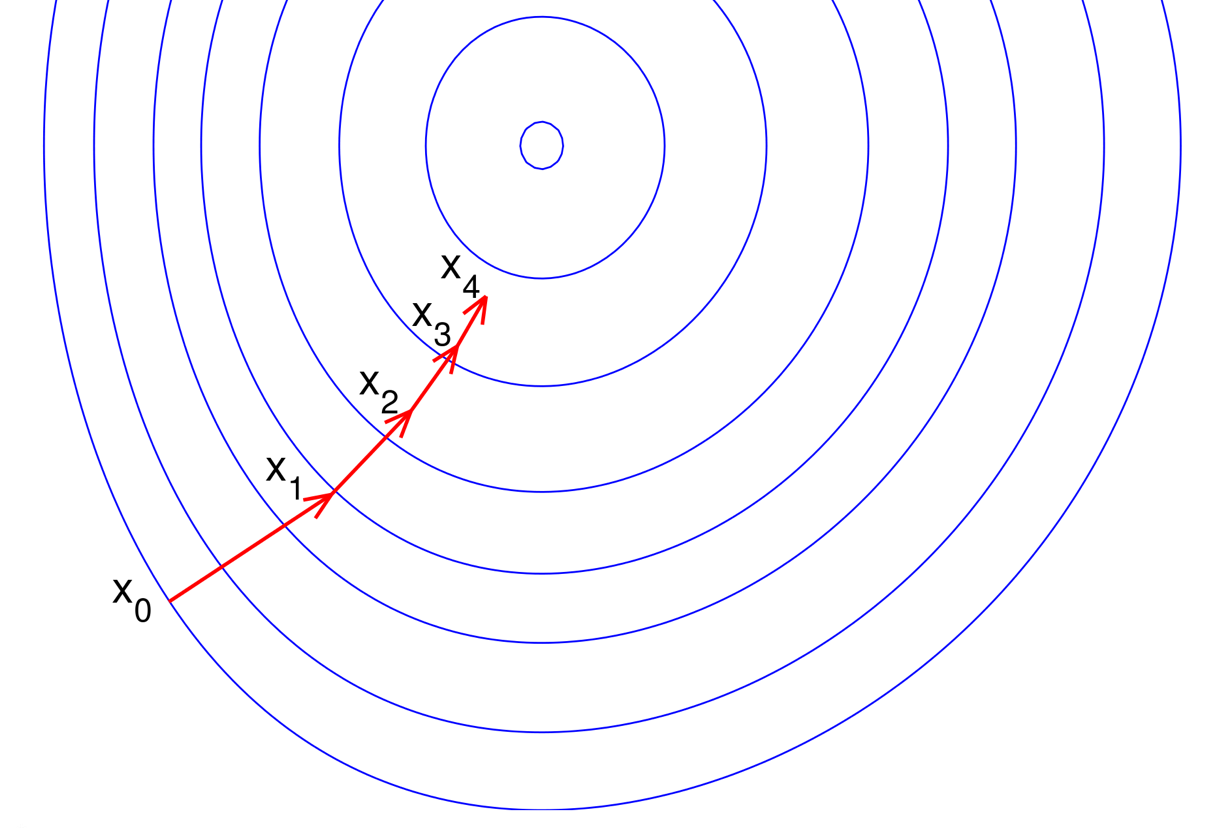
Numerical Optimization Understanding L Bfgs Aria42

1 L Bfgs And Delayed Dynamical Systems Approach For Unconstrained Optimization Xiaohui Xie Supervisor Dr Hon Wah Tam Ppt Download

The Flow Chart Of L Bfgs Method Download Scientific Diagram

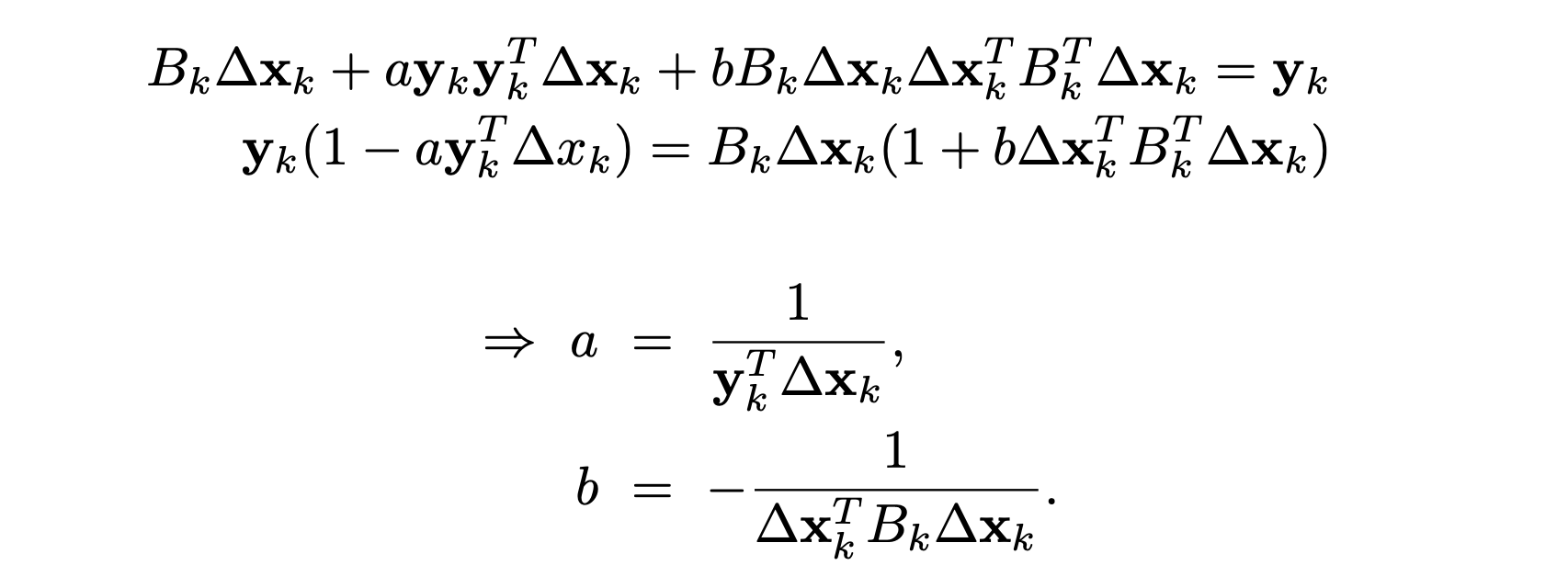
Bfgs In A Nutshell An Introduction To Quasi Newton Methods By Adrian Lam Towards Data Science

1 L Bfgs And Delayed Dynamical Systems Approach For Unconstrained Optimization Xiaohui Xie Supervisor Dr Hon Wah Tam Ppt Download

The L Bfgs Two Loop Recursion Algorithm For Calculating The Action Of Download Scientific Diagram

1 L Bfgs And Delayed Dynamical Systems Approach For Unconstrained Optimization Xiaohui Xie Supervisor Dr Hon Wah Tam Ppt Download

Bfgs And L Bfgs Materials Czxttkl

The Flow Chart Of L Bfgs Method Download Scientific Diagram